|
(iii) Body of mass M placed on a platform having
a downward acceleration a
The platform can not accelerate the body downwards. The body
has to use part of its weight to accelerate itself.
The body exerts a force M(g -a) on the platform. The
platform exerts the same force.
Reaction R = M(g - a)
NB: A downward acceleration has the same effect as
an upward retardation.
(iv) Mass m placed on an inclined plane.

Note: All bodies placed or moving on an incline experience
a force mgsinq down the
plane.
(v) Connected bodies (m1 > m2 )
NB: connected bodies move with a common acceleration.
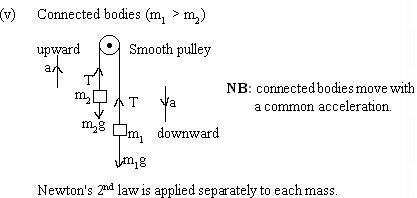
Newton's 2nd law is applied separately to each
mass.
For mass m2: Net upward force = T - m2g
= m2a.
m2a = T - m2g ----------------------
(1)
For mass m1 : Net downward force = m1g
- T = m1a
m1a = m1g - T ---------------(2)
Eq(1) + Eq(2)
(m1 + m2) a = (m1 -m2)g
a = (m1 - m2)g / (m1
+ m2)
WORKED EXAMPLES
1(a) A body of mass 30 kg lies on a smooth table at a distance
of 10 m from the edge of the table.
The mass is connected to another of mass 10 kg by a
light inelastic string passing over a small
smooth pulley at the edge of the table.
Find:
(i) the acceration of the system
(ii) the tension in the string
(iii) the time taken for the 30 kg mass
to reach the edge of the table.
(b) P is a smooth fixed pulley , over which
passes a light inextensible string. Each end of the string
supports a scale pan of mass m kg. One scale pan
contains a particle of mass m1 kg, the other
contains a particle of mass m2 kg.
Given m1 > m2.
(i) Determine an expression for the magnitude of the acceleration
of the scale pan and its contents.
(ii) Show that the reaction R1 of the scale pan
on the particle of mass m1 kg is given by
R = 2m1 (m + m2 )g/ (2m + m1
+ m2 )
(c) Sand is deposited at a uniform rate of 20 kgs-1
and with negligible kinetic energy onto an empty conveyor
belt moving horizontally at a constant speed of 10 m per minute.
Find
(i) the force required to maintain the constant velocity.
(ii) the power required to maintain the constant velocity.
(iii) the rate of change kinetic energy of the moving sand.
Why are the latter two quantities unequal.
2(a)(i) State Newton's law of motion.
(ii) A man of mass 80 kg stands on a platform of mass 40
kg. He pulls a rope that is fastened to the platform and runs
over a pulley on the ceiling. With what force does he have
to pull in order to give himself and the platform an upward
acceleration of 1ms-2?
b(i) Water leaves a hose at a rate of 5.0 kgs-1
with a speed of 20m/s and is directed horizontally on a vertical
wall which stops it.
Calculate the force exerted by the water on the wall.
(ii) Rain is falling vertically at 8.0 ms-1 relative
to the ground. The rain drops make tracks on the side window
of a car at an angle of 30° below the horizontal.
Calculate the speed of the car.
c(i) State the work-energy theorem.
(ii) The fig. below shows three forces acting on a particle
P of mass
5 kg initially at rest.
Determine the magnitude and direction of the of
resultant force on the particle and its kinetic energy after
moving 10 m.
(d) A rectangular block of mass 10.0 kg is pulled from rest
along a smooth inclined plane by a light inelastic string
which passes over a light frictionless pulley P, and carries
a mass of 20.0 kg as shown in the figure below.
The inclined plane makes an angle of 300
with the horizontal.
Determine
(i) the acceleration of the block.
(ii) the tension T, in the string.
(iii) the kinetic energy of the 10 kg block when it has moved
a distance of 2 m along the inclined plane.
|


